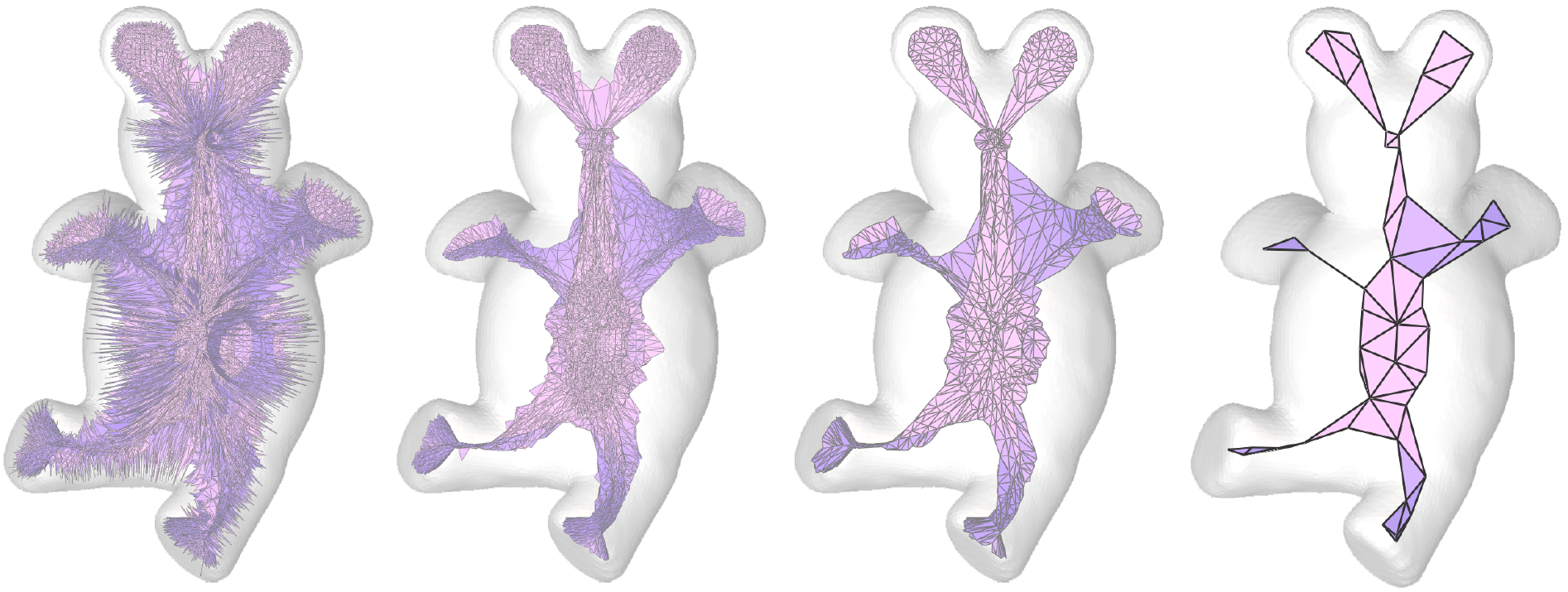
Q-MAT: Computing Medial Axis Transform by Quadratic Error Minimization

The medial axis transform (MAT) is an important shape representation for shape approximation, shape recognition, and shape retrieval. Despite years of research, there is still a lack of effective methods for efficient, robust and accurate computation of the MAT. We present an efficient method, called Q-MAT, that uses quadratic error minimization to compute a structurally simple, geometrically accurate, and compact representation of the MAT. We introduce a new error metric for approximation and a new quantitative characterization of unstable branches of the MAT, and integrate them in an extension of the well-known quadric error metric (QEM) framework for mesh decimation. Q-MAT is fast, removes insignificant unstable branches effectively, and produces a simple and accurate piecewise linear approximation of the MAT. The method is thoroughly validated and compared with existing methods for MAT computation.

Paper [preprint pdf], Video [mp4], Executable Program [zip] Source code[rar]

We would like to thank Kanglai Qian and Yingya Wei for helping preparing the video and some illustrations, and the anonymous reviewers for valuable suggestions. The models we use in our paper are provided by the database of [Chen et al. 2009] and Aim-at-Shape. This project was partially funded by National Basic Research Program of China (2011CB302400), National Science Foundation of China (61373071, 61272019 and 61332015), and the Research Grant Council of Hong Kong (718311 and 717813). Xiaohu Guo is partially supported by Cancer Prevention & Research Institute of Texas (CPRIT) under Grant No. RP110329, and National Science Foundation (NSF) under Grant Nos. IIS-1149737 and CNS-1012975.